Question

A new school has x day students and y boarding students.

The fees for a day student are $600 a term.
The fees for a boarding student are $1200 a term.
The school needs at least $720 000 a term.
Show that this information can be written as x + 2y ≥ 1200.​

Answer 1

Given:

The fees for a day student are $600 a term.

The fees for a boarding student are $1200 a term.

The school needs at least $720000 a term.

To show:

That the given information can be written as
`x + 2y\geq 1200`.​

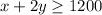Solution:

Let x be the number of day students and y be the number of boarding students.

The fees for a day student are
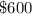`\$600` a term.

So, the fees for
`x` day students are
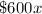`\$600x` a term.

The fees for a boarding student are
`\$1200` a term.

The fees for
`y` boarding student are
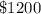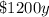`\$1200y` a term.

Total fees for
`x` day students and
`y` boarding student is:

`\text{Total fees}=600x+1200y`

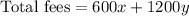
The school needs at least $720000 a term. It means, total fees must be greater than or equal to $720000.

`600x+1200y\geq 720000`

`600(x+2y)\geq 720000`

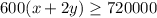
Divide both sides by 600.

`(600(x+2y))/(600)\geq (720000)/(600)`

`x+2y\geq 1200`

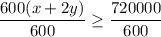
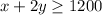
Hence proved.