Answer:
The expected radius of the Earth is 3.883 meters.
Step-by-step explanation:
The formula for the escape speed is derived from Principle of Energy Conservation and knowing that rocket is initially at rest on the surface of the Earth and final energy is entirely translational kinetic, that is:
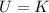 (1)
(1)
Where:
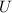 - Gravitational potential energy, in joules.
- Gravitational potential energy, in joules.
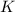 - Translational kinetic energy, in joules.
- Translational kinetic energy, in joules.
Then, we expand the formula by definitions of potential and kinetic energy:
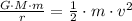 (2)
(2)
Where:
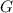 - Gravitational constant, in cubic meters per kilogram-square second.
- Gravitational constant, in cubic meters per kilogram-square second.
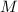 - Mass of the Earth. in kilograms.
- Mass of the Earth. in kilograms.
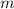 - Mass of the rocket, in kilograms.
- Mass of the rocket, in kilograms.
 - Radius of the Earth, in meters.
- Radius of the Earth, in meters.
 - Escape velocity, in meters per second.
- Escape velocity, in meters per second.
Then, we derive an expression for the escape velocity by clearing it within (2):
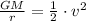
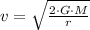 (3)
(3)
If we know that
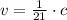 ,
,
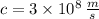 ,
,
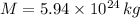 ,
,
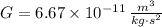 and
and
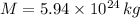 , then the expected radius of the Earth is:
, then the expected radius of the Earth is:
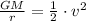
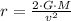
![r = (2\cdot \left(6.67* 10^(-11)\,(m^(3))/(kg\cdot s^(2)) \right)\cdot (5.94* 10^(24)\,kg))/(\left[(1)/(21)\cdot \left(3* 10^(8)\,(m)/(s) \right) \right]^(2))](https://img.qammunity.org/2022/formulas/physics/college/e6s7ylnk3xiuphtm2ntma0l5wcdf4cwamz.png)
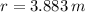
The expected radius of the Earth is 3.883 meters.