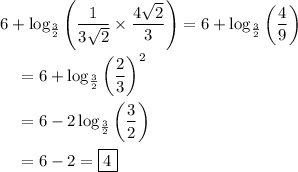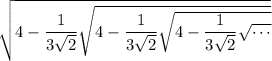
Starting from the identity
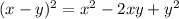
take the positive square root on both sides.
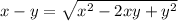
Note that we must have
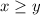 . Rewrite the radicand and substitute
. Rewrite the radicand and substitute
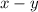 .
.
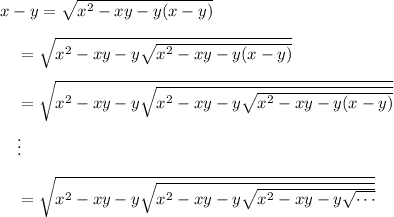
Let
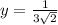 . Solve for
. Solve for
 .
.
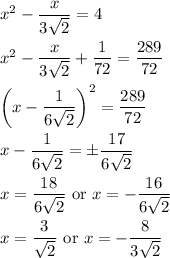
Take the positive solution to ensure
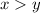 . Then the infinitely nested root expression in the logarithm converges to
. Then the infinitely nested root expression in the logarithm converges to
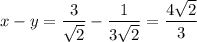
and the overall expression has a value of