Question

For a group of 50 people, what is the probability that at least two of them have the same birthday(excluding year). assume that there are 365 days of the year, and using a formula to represent the result is acceptable.

Answer 1

The probability is 0.97

Explanation:

The probability that at least two of them have the same birthday, is equal to:

1 - P

where we define P as the probability where all of the 50 people have different birthdays.

So we just need to calculate P, which is equal to the quotient between the combinations where all 50 people have different birthdays, and the total number of combinations, that is just:

total = (365)^50

For the combinations where all of them have different birthdays, we just need to find the number of options for each person.

The first person's birthday can be any of the 365 days.

for the second person, we have 364 days, because one day was already taken by the first person.

For the third person there are 363 days, and so on.

And we know that the total number of combinations is equal to the product between the number of possible options, so here the combinations are:

C = 365*(364)*(363)*(362)*...*(365 - 49) = 365!/(365 - 50)!

Then the value of P is just:

`P = (C)/(total) = (365!)/((365 - 50)!) *(1)/(365^(50)) = 0.0296`

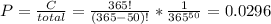
Then the probability that, at least two, of the 50 people have the same birthday is:

Probability = 1 - P = 1 - 0.0296 = 0.9704

Which we can round just to 0.97, or 97% in percentage form.