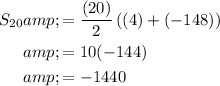Answer:
The sum of the first 20 terms is -1440.
Explanation:
We want to find the sum of the first 20 terms of the arithmetic sequence:
4, -4, -12, -20...
The sum of an arithmetic sequence is given by:
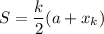
Where k is the number of terms, a is the initial term, and x_k is the last term.
Since we want to find the sum of the first 20 terms, k = 20.
Our initial term a is 4.
Our last term is also the 20th term as we want the sum of the first 20 terms.
To find the 20th term, we can write an explicit formula for our sequence. The explicit formula for an arithmetic sequence is given by:
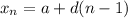
Where a is the initial term, d is the common difference, and n is the nth term.
Our initial term is 4. From the sequence, we can see that our common difference is -8 since each subsequent term is eight less than the previous term. Therefore:
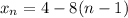
Then the last or 20th term is:
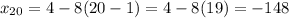
Therefore, the sum of the first 20 terms are: