Question

The angular velocity of an object is given by the following equation: ω(t)=(5rads3)t2\omega\left(t\right)=\left(5\frac{rad}{s^3}\right)t^2ω(t)=(5s3rad​)t2 What is the angular displacement of the object (in rad) between t = 2 s and t = 4 s?

Answer 1

The angular displacement of the object between
`t = 2\,s` and
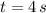`t = 4\,s` is 20 radians.

Step-by-step explanation:

The angular velocity of the object (
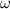`\omega`), in radians per second, is given by the following expression:

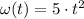`\omega(t) = 5\cdot t^(2)` (1)

Where
`t` is the time, measured in seconds.

The change in the angular displacement (
`\Delta \theta`), in radians, is found by means of the following definite integral:

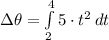`\Delta \theta = \int\limits^(4)_(2) {5\cdot t^(2)} \, dt` (2)

Then we proceed to integrate on the function in time:

`\Delta \theta = (5)/(3)\cdot (4^(2)-2^(2))`

`\Delta \theta = 20\,rad`

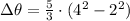
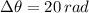
The angular displacement of the object between
`t = 2\,s` and
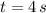`t = 4\,s` is 20 radians.