Question

Multiplicative inverse of (7/3)^-3

Answer 1

Hi there! I am EnjoyingLife, and I hope you find my answer helpful! :)

STEPS:

First we have a negative power so we flop the number over

Then since we have a fraction to a power we raise both the top & bottom to that power.

Then, we flop the number over once more to find the multiplicative inverse.

Hope it helps!

Answer 2

Hello.

First, let's calculate

`\tt{\displaystyle((7)/(3)) ^(-3)`

Remember the Properties of Exponents:

If we have a number to a negative power, we flop the number over:

`\tt{a^(-b)=\displaystyle(1)/(a^b)`

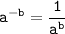
Now, let's use this property to simplify our expression.

Flop the number over:

`\tt{\displaystyle((3)/(7) )^3`

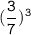
Now, we should recall another property of exponents:

`\tt{\displaystyle((a)/(b) )^m=(a^m)/(b^m)`

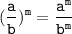
Since we have a fraction to a power, we should raise both the numerator and the denominator to the power:

`\tt{\displaystyle(3^3)/(7^3)`

3 cubed is 9, and 7 cubed is 343:

`\tt{\displaystyle(9)/(343)`

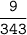
Now, the multiplicative inverse of that number is simply that number flopped over:

`\Large\boxed{\tt{\displaystyle(343)/(9) }}`

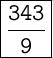
I hope it helps.

Have a great day.

`\boxed{imperturbability}`