Answer:
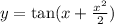
Explanation:
Poorly formatted question; The complete question requires that we prove that
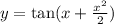
When
 and
and
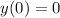
We have:

Rewrite as:
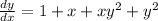
Factorize
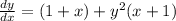
Rewrite as:
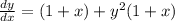
Factor out 1 + x
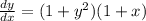
Multiply both sides by
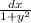

Integrate both sides
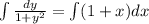
Rewrite as:
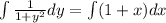
Integrate the left-hand side

Integrate the right-hand side
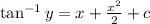
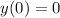 implies that:
implies that:
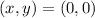
So:
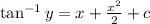 becomes
becomes
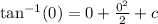
This gives:
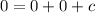
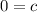
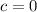
The equation
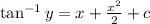 becomes
becomes
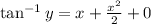
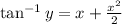
Take tan of both sides
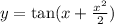 --- Proved
--- Proved