Answer:
132 people bought balcony seats and 450 people bought ground seats.
Explanation:
We want to solve the system of equations:
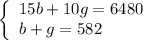
We can solve this by using substitution. From the second equation, we can subtract b from both sides:
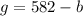
In the first equation, we can divide both sides by five:
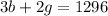
Substitute:
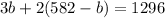
Distribute:

Simplify:
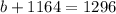
Solve for b:
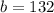
Using the modified equation again, substitute:
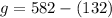
Evaluate:
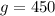
Therefore, 132 people bought balcony seats and 450 people bought ground seats.