Answer:
The standard deviation of the sampling distribution of sample means would be 0.8186.
Explanation:
We are given that
Mean of population=23.2 pounds
Standard deviation of population=6.6 pounds
n=65
We have to find the standard deviation of the sampling distribution of sample means.
We know that standard deviation of the sampling distribution of sample means
=
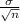
Using the formula
The standard deviation of the sampling distribution of sample means
=
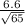
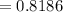
Hence, the standard deviation of the sampling distribution of sample means would be 0.8186.