Answer:
The cutoff time be for concert setup should be of 51.4 minutes.
Explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Average time it takes their sound tech to set up for a show is 56.1 minutes, with a standard deviation of 6.4 minutes.
This means that
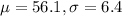
If the band manager decides to include only the fastest 23% of sound techs on the tour, what should the cutoff time be for concert setup?
The cutoff time would be the 23rd percentile of times, which is X when Z has a p-value of 0.23, so X when Z = -0.74.

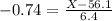
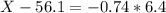
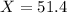
The cutoff time be for concert setup should be of 51.4 minutes.