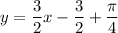Question

Please help me with solving these. I’d really appreciate your help. Thank you very much.

Answer 1

Problem 17)

`\displaystyle y=-(5)/(2)x+(7)/(2)`

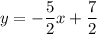
Problem 18)

`\displaystyle y=(3)/(2)x-(3)/(2)+(\pi)/(4)`

Explanation:

Problem 17)

We have the curve represented by the equation:

`\displaystyle 4x^2+2xy+y^2=7`

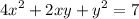
And we want to find the equation of the tangent line to the point (1, 1).

First, let's find the derivative dy/dx. Take the derivative of both sides with respect to x:

`\displaystyle (d)/(dx)\left[4x^2+2xy+y^2\right]=(d)/(dx)[7]`

Simplify. Recall that the derivative of a constant is zero.

`\displaystyle (d)/(dx)[4x^2]+(d)/(dx)[2xy]+(d)/(dx)[y^2]=0`

Differentiate. We can differentiate the first term normally. The second term will require the product rule. Hence:

`\displaystyle 8x+\left(2y+2x(dy)/(dx)\right)+2y(dy)/(dx)=0`

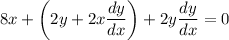
Rewrite:

`\displaystyle (dy)/(dx)\left(2x+2y\right)=-8x-2y`

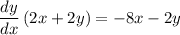
Therefore:

`\displaystyle (dy)/(dx)=(-8x-2y)/(2x+2y)=-(4x+y)/(x+y)`

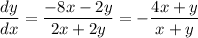
So, the slope of the tangent line at the point (1, 1) is:

`\displaystyle (dy)/(dx)\Big|_((1, 1))=-(4(1)+(1))/((1)+(1))=-(5)/(2)`

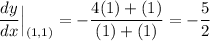
And since we know that it passes through the point (1, 1), by the point-slope form:

`\displaystyle y-1=-(5)/(2)(x-1)`

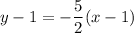
If desired, we can simplify this into slope-intercept form. Therefore, our equation is:

`\displaystyle y=-(5)/(2)x+(7)/(2)`

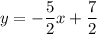
Problem 18)

We have the equation:

`\displaystyle y=\tan^(-1)\left(x^3\right)`

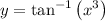
And we want to find the equation of the tangent line to the graph at the point (1, π/4).

Take the derivative of both sides with respect to x:

`\displaystyle (dy)/(dx)=(d)/(dx)\left[\tan^(-1)(x^3)]`

We can use the chain rule:

`\displaystyle (d)/(dx)[u(v(x))]=u'(v(x))\cdot v(x)`

Let u(x) = tan⁻¹(x) and let v(x) = x³. Thus:

(Recall that d/dx [arctan(x)] = 1 / (1 + x²).)

`\displaystyle (d)/(dx)\left[\tan^(-1)(x^3)\right]=(1)/(1+v^2(x))\cdot 3x^2`

Substitute and simplify. Hence:

`\displaystyle (d)/(dx)\left[\tan^(-1)(x^3)\right]=(1)/(1+v^2(x))\cdot 3x^2=(3x^2)/(1+x^6)`

Then the slope of the tangent line at the point (1, π/4) is:

`\displaystyle (dy)/(dx)\Big|_(x=1)=(3(1)^2)/(1+(1)^6)=(3)/(2)`

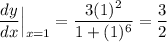
Then by the point-slope form:

`\displaystyle y-(\pi)/(4)=(3)/(2)(x-1)`

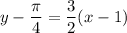
Or in slope-intercept form:

`\displaystyle y=(3)/(2)x-(3)/(2)+(\pi)/(4)`