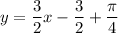Answer:
Problem 17)
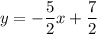
Problem 18)
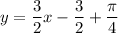
Explanation:
Problem 17)
We have the curve represented by the equation:
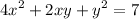
And we want to find the equation of the tangent line to the point (1, 1).
First, let's find the derivative dy/dx. Take the derivative of both sides with respect to x:
![\displaystyle (d)/(dx)\left[4x^2+2xy+y^2\right]=(d)/(dx)[7]](https://img.qammunity.org/2022/formulas/mathematics/college/31nddfd6avtnjdbs6jc4imnnv6onczf60a.png)
Simplify. Recall that the derivative of a constant is zero.
![\displaystyle (d)/(dx)[4x^2]+(d)/(dx)[2xy]+(d)/(dx)[y^2]=0](https://img.qammunity.org/2022/formulas/mathematics/college/o4qjlvlbzm38um493ww3y8aecynzjn6c28.png)
Differentiate. We can differentiate the first term normally. The second term will require the product rule. Hence:
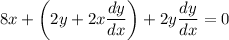
Rewrite:
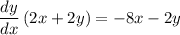
Therefore:
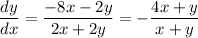
So, the slope of the tangent line at the point (1, 1) is:
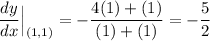
And since we know that it passes through the point (1, 1), by the point-slope form:
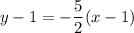
If desired, we can simplify this into slope-intercept form. Therefore, our equation is:
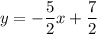
Problem 18)
We have the equation:
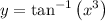
And we want to find the equation of the tangent line to the graph at the point (1, π/4).
Take the derivative of both sides with respect to x:
![\displaystyle (dy)/(dx)=(d)/(dx)\left[\tan^(-1)(x^3)]](https://img.qammunity.org/2022/formulas/mathematics/college/df9pbmz4pdmm8c4d0bwf94ttv2fc6iupue.png)
We can use the chain rule:
![\displaystyle (d)/(dx)[u(v(x))]=u'(v(x))\cdot v(x)](https://img.qammunity.org/2022/formulas/mathematics/college/wb3zs06f9n91qmkqvwafe5cmfvrr988tte.png)
Let u(x) = tan⁻¹(x) and let v(x) = x³. Thus:
(Recall that d/dx [arctan(x)] = 1 / (1 + x²).)
![\displaystyle (d)/(dx)\left[\tan^(-1)(x^3)\right]=(1)/(1+v^2(x))\cdot 3x^2](https://img.qammunity.org/2022/formulas/mathematics/college/xn7xfh4lzcf8i6kpc8s24z4gph47ynu9um.png)
Substitute and simplify. Hence:
![\displaystyle (d)/(dx)\left[\tan^(-1)(x^3)\right]=(1)/(1+v^2(x))\cdot 3x^2=(3x^2)/(1+x^6)](https://img.qammunity.org/2022/formulas/mathematics/college/6forb96hybcyj1doxqofvoiqvhh3qh0v88.png)
Then the slope of the tangent line at the point (1, π/4) is:
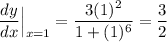
Then by the point-slope form:
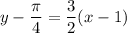
Or in slope-intercept form: