Hey there!
We are given two functions - one is Exponential while the another one is Linear.
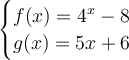
1. Operation of Function
- (f+g)(x) is a factored form of f(x)+g(x). We can common factor out x. Therefore:
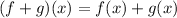
2. Substitution
- Next, we substitute f(x) = 4^x+8 and g(x) = 5x+6.
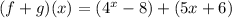
3. Evaluate/Simplify
- Cancel out the brackets and combine like terms.
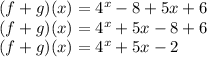
4. Final Answer