Answer:
The number of revolutions is 44.6.
Step-by-step explanation:
We can find the revolutions of the wheel with the following equation:
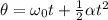
Where:
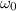 : is the initial angular velocity = 13 rad/s
: is the initial angular velocity = 13 rad/s
t: is the time = 8 s
α: is the angular acceleration
We can find the angular acceleration with the initial and final angular velocities:
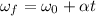
Where:
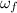 : is the final angular velocity = 57 rad/s
: is the final angular velocity = 57 rad/s

Hence, the number of revolutions is:
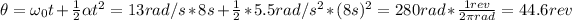
Therefore, the number of revolutions is 44.6.
I hope it helps you!