Answer:

Explanation:
We can solve this multiplication of polynomials by understanding how to multiply these large terms.
To multiply two polynomials together, we must multiply each term by each term in the other polynomial. Each term should be multiplied by another one until it's multiplied by all of the terms in the other expression.
- We can do this by focusing on one term in the first polynomial and multiplying it by all the terms in the second polynomial. We'd then repeat this for the remaining terms in the second polynomial.
Let's first start by multiplying the first term of the first polynomial,
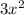 , by all of the terms in the second polynomial. (
, by all of the terms in the second polynomial. (
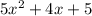 )
)
Now, we can add up all these expressions to get the first part of our polynomial. Ordering by exponent, our expression is now
Now let's do the same with the second term (
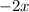 ) and the third term (
) and the third term (
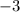 ).
).
- Adding on to our original expression:
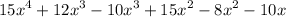
- Adding on to our original expression:
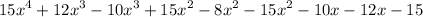
Phew, that's one big polynomial! We can simplify it by combining like terms. We can combine terms that share the same exponent and combine them via their coefficients.
This simplifies our expression down to
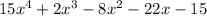 .
.
Hope this helped!