Question

A casserole is removed from a 375oF oven and cools to 190oF after 25 minutes in a room at 68oF. How long (from the time it is a removed from the oven) will it take the casserole to cool to 105oF

Answer 1

57.3 minutes

Explanation:

We know that the temperature as a function of time of an object is described by the equation:

`T(t) = T_a + (T_0 - Ta)*e^(-k*t)`

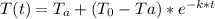
Where:

k is a constant

Tₐ = room temperature = 68°F

T₀ = initial temperature of the object = 375°F

Replacing these in our equation we will get

T(t) = 68°F + (375°F - 68°F)*e^{-k*t} = 68°F + (307°F)*e^{-k*t}

And we know that after 25 minutes, at t = 25min, the temperature of the casserole is 190°F

then:

T(25min) = 190°F = 68°F + (307°F)*e^{-k*25 min}

Now we can solve this for k:

190°F = 68°F + (307°F)*e^{-k*25 min}

190°F - 68°F = (307°F)*e^{-k*25 min}

(122°F)/(307°F) = e^{-k*25 min}

Now we can apply the natural logarithm in both sides:

Ln( 122/307) = Ln(e^{-k*25 min}) = -k*25min

Ln( 122/307)/(-25 min) = k = 0.0369 min^-1

Then the temperature equation is:

T(t) = 68°F + (307°F)*e^{-0.0369 min^-1*t}

Now we want to find the value of t such that:

T(t) = 105°F = 68°F + (307°F)*e^{-0.0369 min^-1*t}

We can solve this in the same way:

105°F - 68°F = (307°F)*e^{-0.0369 min^-1*t}

37°F = (307°F)*e^{-0.0369 min^-1*t}

(37°F)/(307°F) = e^{-0.0369 min^-1*t}

Ln( 37/307) = -0.0369 min^-1*t

Ln( 37/307)/( -0.0369 min^-1 ) = 57.3 min

So after 57.3 minutes, the temperature of the casserrole will be 105°F