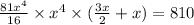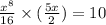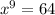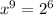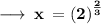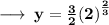Question

A system equation is-


`\bf\begin{cases} & \bf x^4y^5+x^5y^4=810 \\ & \bf x^6y^3+x^3y^6=945 \end{cases}`

​

​


Solve for real x and y .
How to solve it? Please explain. The question is correct.​

Answer 1

Solution:

Given that,

x⁴y⁵ + x⁵y⁴ = 810

➝ x⁴y⁴(x+y) = 810 ---(1)

`\:`

Further given that,

x⁶y³ + x³y⁶ = 945

x³y³(x³y³) = 945

`\:`

We know,

`{ \boxed{{x}^(3) + {y}^(3) = (x + y)( {x}^(2) - xy + {y}^(2)) }}`

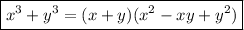
So, using this identity, we get,

➝ x³y³( x + y )( x² - xy + y²) = 945

---(2)

`\:`

On dividing equation (1) and (2), we get,

`\longrightarrow\frac{ {x}^(2) - xy + {y}^(2) }{xy} = (945)/(810)`

`\longrightarrow \: \frac{ {x}^(2) + {y}^(2) }{xy} - 1 = (7)/(6)`

`\longrightarrow \: \frac{ {x}^(2) + {y}^(2) }{xy} = (7)/(6) + 1`

`\longrightarrow \: \frac{ {x}^(2) + {y}^(2) }{xy} = (7 + 6)/(6)`

`\longrightarrow \: \frac{ {x}^(2) + {y}^(2) }{xy} = (13)/(6)`

`\:`

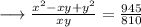
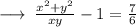
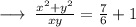
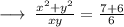
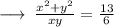
➝ 6x² + 6y² = 13xy

➝ 6x² - 13xy + 6y² = 0

➝ 6x² - 4xy - 9xy + 6y² = 0

➝ 2x( 3x - 2y ) - 3y( 3x - 2y ) = 0

➝ ( 3x - 2y ) ( 2x - 3y ) = 0

`\longrightarrow \:{ \bold{ x = (3y)/(2) \: \: \: or \: \: x = (2y)/(3) }}`

`\:`

`\:`

`{ \underline {\underline {\red{Case:- 1 }}}}`

`{ \bold{When \: x = (3y)/(2)}}`

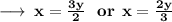
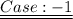
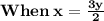
In Substating the value of x in equation (1) we get,

`\frac{81 {y}^(4) }{16} * {y}^(4) * ( (3y)/(2) + y) = 810`

`\frac{ {y}^(8) }{16} * ( (5y)/(2) ) = 10`

`{y}^(9) = 64`

`{y}^(9) = {2}^(6)`

`\:`

`\longrightarrow \: { \bold{y = {(2)}^{ (2)/(3) } }}`

`\longrightarrow \: { \bold{x = (3)/(2) {(2)}^{ (2)/(3) } }}`

`\:`

`\:`

`{ \underline {\underline {\red{Case:- 2}}}}`

`{ \bold{When \: x \: = (2y)/(3) \rightarrow \: \: y = (3x)/(2) }}`

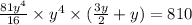
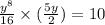
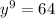
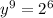
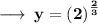
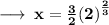
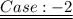
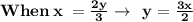
On Substituting the value of y in equation (2), we get,

`\frac{81 {x}^(4) }{16} * {x}^(4) * ( (3x)/(2) + x) = 810`

`\frac{ {x}^(8) }{16} * ( (5x)/(2) ) = 10`

`{x}^(9) = 64`

`{x}^(9) = {2}^(6)`

`\:`

`\longrightarrow \: { \bold{x \: = {(2)}^{ (2)/(3) } }}`

`\longrightarrow \: { \bold{y = (3)/(2) {(2)}^{ (2)/(3) } }}`