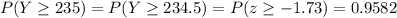Answer:
(a)

The standard deviation is
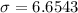
(b)
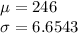
Here sample size is large and np and n(1-p) are both greater than 30. So we can use a normal approximation of binomial distribution. z-score for Y = 234.5 (using continuity correction) is
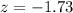
So the approximate probability that at least 235 people in the sample will still be in the Rewards Program after the first four weeks is
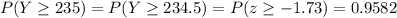
Explanation:
Let X is a random variable that shows the number of people who would drop out of the Rewards Program within four weeks. Here X has binomial distribution with parameters n = 300 and p = 0.18.
(a)
The mean number of people who would drop out of the Rewards Program within four weeks in a sample of this size is
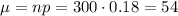
The standard deviation is

(b)
Let Y is a random variable that shows the number of people in the sample who will still be in the Rewards Program after the first four weeks. Here Y has a binomial distribution with parameters n= 300 and p=0.82. So mean of Y is

Here sample size is large and np and n(1-p) are both greater than 30. So we can use a normal approximation of binomial distribution. z-score for Y = 234.5 (using continuity correction) is
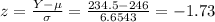
So the approximate probability that at least 235 people in the sample will still be in the Rewards Program after the first four weeks is