Step-by-step explanation:
Need to FinD :
- The velocity of the ball with strikes the ground.
- The time of the ball after which it strikes the ground.

We know that,
- The ball is dropped from the height of 30 m as stated in the question. Therefore, it will have a initial velocity of 0 m/s. The distance travelled by the ball will be 30 metres as the distance travelled by the ball is equal to the height of the tower and that is 30 metres.
So, by using the third equation of motion, we will find out the final velocity of the ball.

Therefore,

∴ Hence, the required final velocity of the ball with which it strikes the ground is 24.5 m/s. Since, we know that the initial velocity of the ball is 0 m/s and the acceleration of the ball is 10 m/s². So, by using the first equation of motion, we will find out the time of the ball after which it stikes the ground.

Therefore,
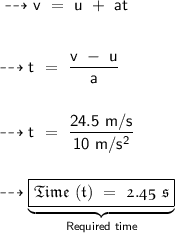
∴ Hence, the required time of the ball after which it strikes the ground is 2.45 seconds.