Answer:
Step-by-step explanation:
The first thing we are asked to find is the Force experienced by the box. That is found in the formula:
F - f = ma where F is the force exerted by the box, f is the friction opposing the box, m is the mass, and a is the acceleration (NOT the same as the pull of gravity). But F can be rewritten in terms of the angle of inclination also:
 where w is the weight of the box. We will use this version of the formula because it will help us answer the second question, which is to solve for a. Filling in:
where w is the weight of the box. We will use this version of the formula because it will help us answer the second question, which is to solve for a. Filling in:
First we need the weight of the box. Having the mass, we find the weight:
w = mg so
w = 25.14(10) so
w = 251.4 N (I am not paying any attention at all to the sig fig's here, since I noticed no one on this site does!) Now we have the weight. Filling that in:
251.4sin(30) - f = ma Before we go on to fill in for f, let's answer the first question. F = 251.4sin(30) so
F = 125.7 And in order to answer what a is equal to, we find f:
f = μ
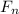 where Fn is the weight of the object.
where Fn is the weight of the object.
f = .25(251.4) so
f = 62.85. Filling everything in now altogether to solve for a, the only missing value:
125.7 - 62.85 = 25.14a and
62.85 = 25.14a so
a = 2.5 m/s/s
Now we have to move on to another set of equations to answer the last part. The last part involves the y-dimension. In this dimension, what we know is that
a = -10 m/s/s
v₀ = 0 (it starts from rest)
Δx = -13.30 m (negative because the box falls this fr below the point fro which it started). Putting all that together in the equation for displacement:
Δx = v₀t +
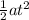 and we are solving for time:
and we are solving for time:
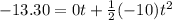 and
and
 so
so
t = 1.6 seconds to reach the bottom of the slope from 13.30 m high.