Question

Solve for x. 4x-4< 8
AND 9x +5 > 23
is it a, b,c or d ?

Answer 1

`A)\displaystyle2 < x < 3`

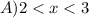
Explanation:

A compound inequality is an inequality that combines two simple inequalities

we are given that

`\displaystyle 4x - 4 < 8 \ \: \text{and} \: \: 9x + 5 > 23`

solving x for the first equation:

`\displaystyle 4x - 4 < 8`

add 4 to both sides:

`\displaystyle 4x < 12`

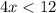
divide both sides by 4 and since we are dividing both sides by a positive number the inequality won't swap

`\displaystyle x < 3`

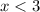
solving x for the second equation:

`\displaystyle 9x + 5 > 23`

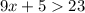
cancel 5 from both sides:

`\displaystyle 9x > 18`

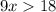
divide both sides by 9 and since we are dividing both sides by a positive number:

`\displaystyle x > 2`

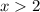
therefore by combining the equations we obtain:

`\displaystyle\boxed{2 < x < 3}`

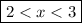
hence,

our answer is A)