Answer:
B
Explanation:
The equation of a circle has the form:

Where (h, k) is the center of the circle and r is the radius.
From the graph, we can see that the center of the circle is at (-5, 0). So, (h, k) is (-5, 0), where h = -5 and k = 0.
And by counting, we can determine that the radius of the circle is three units. Hence, r = 3.
Substitute the information into the equation:
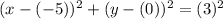
Simplify. Therefore, our equation is:
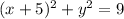
Our answer is B.