Question

Write the quadratic function in the form f (x) = a (x - h)2 + k.

Then, give the vertex of its graph.
f (x) = – 2x² + 16x – 30

Writing in the form specified: f(x)=???

Vertex: (?,?)

Answer 1

The vertex form is:

`f(x)=-2(x-4)^2+2`

Where the vertex of the function is (4, 2).

Explanation:

We want to find the vertex and the vertex form of the quadratic function:

`f(x)=-2x^2+16x-30`

We have two methods of converting from standard form to vertex form: (1) by using the vertex formulas or (2) by completing the square.

Method 1) Using Formulas:

First, note that the leading coefficient of our function is -2.

The vertex of a quadratic equation is given by the formulas:

`\displaystyle \text{Vertex}=\left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

In this case, a = -2, b = 16, and c = -30. Find the x-coordinate of the vertex:

`\displaystyle x=-((16))/(2(-2))=(-16)/(-4)=4`

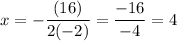
In order to find the y-coordinate of the vertex, we substitute this value back in. Hence:

`f(4)=-2(4)^2+16(4)-30=2`

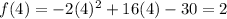
Therefore, our vertex is (4, 2).

Vertex form is:

`\displaystyle f(x)=a(x-h)^2+k`

Where a is the leading coefficient and (h, k) is the vertex.

Substitute. Our leading coefficient is -2 and our vertex is (4, 2). Therefore:

`\displaystyle f(x)=-2(x-4)^2+2`

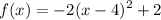
Method 2) Completing the Square:

To complete the square, we first factor out the leading coefficient from the first two terms:

`f(x)=-2(x^2-8x)-30`

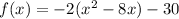
Then, we divide the coefficient of the b term by half and square it. This yields:

`\displaystyle \left((-8)/(2)\right)^2=16`

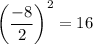
We will add this value inside of the parentheses. Since we added 16 inside the parentheses, we will subtract 16 outside of the parenthese to remain the equality of the function. However, since the parentheses is multiplied by -2, we technically added -2(16) = -32 inside. So, we will subtract -32 outside. Thus:

`f(x)=-2(x^2-8x+16)-30-(-32)`

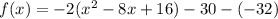
Simplify:

`f(x)=-2(x^2-8x+16)+2`

Factor using the perfect square trinomial:

`f(x)=-2(x-4)^2+2`

We acquire the same result.