Question

Find the equation of Best fit for the data in the table​

Answer 1

The equation of the line is
`y = 2\cdot x + 3`.

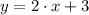Explanation:

The data of the table represents a line, also known as a linear function or a first order polynomial if and only if the following property is satisfied:

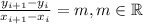`(y_(i+1)-y_(i))/(x_(i+1)-x_(i)) = m, m \in \mathbb{R}` (1)

Now we proceed to check if the table represents a line instead of another kind of function:

`(y_(2)-y_(1))/(x_(2)-x_(1)) = (7-5)/(2-1) = 2`

`(y_(3)-y_(2))/(x_(3)-x_(2)) = (9-7)/(3-2) = 2`

`(y_(4)-y_(3))/(x_(4)-x_(3)) = (13-9)/(5-3) = 2`

`(y_(5)-y_(4))/(x_(5)-x_(4)) = (15-13)/(6-5) = 2`

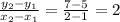
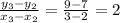
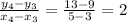
Hence, the data represents a line. From Geometry we know that the equation of the line can be obtained by knowing two distinct points. The formula of the line is described below:

`y = m\cdot x + b` (2)

Where:

`x` - Independent variable.

`y` - Dependent variable.

`m` - Slope.

`b` - y-Intercept.

If we know that
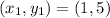`(x_(1), y_(1)) = (1, 5)` and
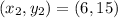`(x_(2), y_(2)) = (6, 15)`, then we have the following system of linear equations:

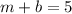`m + b = 5` (1)

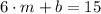`6\cdot m + b = 15` (2)

The solution of the system of linear equations is:
`m = 2`,
`b = 3`.

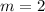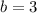The equation of the line is
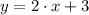`y = 2\cdot x + 3`.