Question

Find the vertex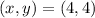, axis of symmetry, y intercept of each parabola. State the number of x intercepts. Then sketch the graph of each function. f(x)=2(x-4)^2+4

Answer 1

Vertex:
`(x,y) = (4,4)`, Axis of symmetry:
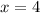`x = 4`, no x-Intercepts, y-Intercepts:
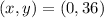`(x,y) = (0, 36)`. The graph is represented in the image attached below.

Explanation:

The equation of the parabola in vertex form and whose axis of symmetry is vertical is described by this formula:

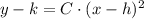`y - k = C\cdot (x-h)^(2)` (1)

Where:

`x` - Independent variable.

`y` - Dependent variable.

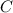`C` - Vertex constant.

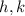`h, k` - Coordinates of the vertex.

By direct comparison, we find the following information:

`h = 4`,
`k = 4`,
`C = 2`

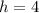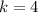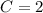
Vertex

The vertex is a point of the parabola so that
`(x,y) = (h, k)`.

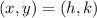If we know that
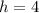`h = 4` and
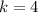`k = 4`, then the coordinates of the vertex are
`(x,y) = (4,4)`.

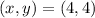Axis of symmetry

The axis of symmetry is a line of the form
`x = h`.

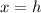If we know that
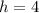`h = 4`, then the axis of symmetry is
`x = 4`.

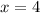To find the x and y intercepts, we need to transform the equation of the parabola into its standards, which is a second grade polynomial:

`y - k = C\cdot (x-h)^(2)`

`y - k = C\cdot (x^(2)-2\cdot h\cdot x +h^(2))`

`y = C\cdot x^(2) -2\cdot C\cdot h \cdot x + (C\cdot h^(2)+k)`

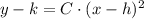
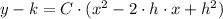
If we know that
`h = 4`,
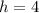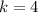`k = 4` and
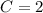`C = 2`, then the equation of the parabola in standard form is:

`y = 2\cdot x^(2)-16\cdot x + 36`

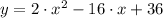
x-Intercepts

The x-intercepts of the polynomial (if exist) can be found by the Quadratic Formula:

`x_(1,2) = \frac{16\pm \sqrt{(-16)^(2)-4\cdot 2\cdot (36)}}{4}`

`x_(1,2) = 4 \pm (√(-32))/(4)`

`x_(1,2) = 4 \pm i \,(4√(2))/(4)`

`x_(1,2) = 4 \pm i\,√(2)`

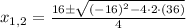
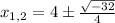
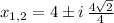
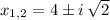
As both roots are conjugated complex numbers, there are no x-intercepts.

y-Intercepts

The y-intercept (if exists) can be found by evaluating the polynomial at
`x = 0`:

`y = 2\cdot 0^(2) - 16\cdot 0 + 36`

`y = 36`

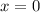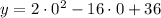
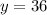
The y-intercept is
`(x,y) = (0, 36)`.

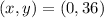Lastly, we proceed to plot the function by using graphing tools.