I use complex analysis to compute the integrals in question.
First, notice that the first integrand is even:

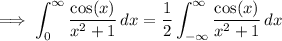
Consider a contour C that's the union of
• Γ, a semicircle of radius R in the upper half-plane, and
• the line segment connecting the points (-R, 0) and (R, 0)
On Γ, we have
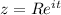 with 0 ≤ t ≤ π.
with 0 ≤ t ≤ π.
Consider the complex function
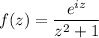
and notice that our original integrand is the real part of f(z). Then the integral of f(z) over C is
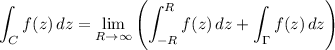
As R → ∞, the first integral on the right is exactly twice the one we want. Estimate the second one to be bounded by
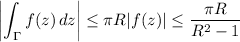
since

and so the integral along Γ vanishes.
f(z) has only one pole in the interior of C at z = i. By the residue theorem,
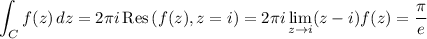
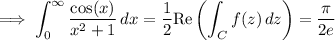
For the second integral, we recall that for complex z,
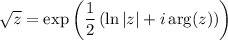
Consider a keyhole contour C, the union of
•
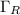 , the larger circle with radius R and
, the larger circle with radius R and
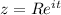 , with 0 < t < 2π ;
, with 0 < t < 2π ;
•
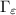 , the smaller circle with radius ε and
, the smaller circle with radius ε and
 , with 0 < t < 2π ;
, with 0 < t < 2π ;
•
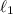 , the line segment above the positive real axis joining
, the line segment above the positive real axis joining
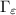 to
to
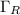 ; and
; and
•
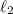 , the other line segment below the positive real axis joining
, the other line segment below the positive real axis joining
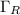 to
to
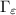
Then
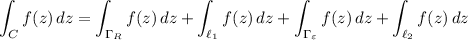
and in the limit, the integral over
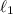 converges to the one we want.
converges to the one we want.
Estimate the integrals over the circular arcs:
•
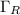 :
:
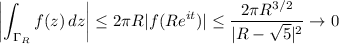
as R → ∞.
•
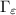 :
:
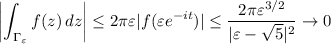
as ε → 0.
Consider the integral over
 :
:
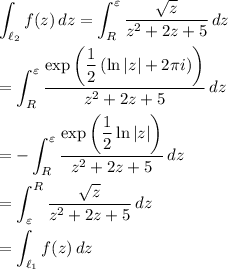
so in fact,
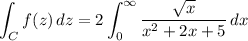
By the residue theorem,
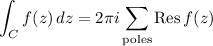
We have poles at z = -1 + 2i and z = -1 - 2i. On our chosen branch,
![√(-1+2i)=i\sqrt[4]{5}\exp\left(-\frac i2\tan^(-1)(2)\right)](https://img.qammunity.org/2023/formulas/mathematics/college/aoi5oo92da7cpp7svhmr29s7sy7h41pbtz.png)
![√(-1-2i)=i\sqrt[4]{5}\exp\left(\frac i2\tan^(-1)(2)\right)](https://img.qammunity.org/2023/formulas/mathematics/college/yfopel6vomnrl5qpp7yn99o1ou04j53ie5.png)
The residues are
![\mathrm{Res}(f(z),z=-1-2i)=\frac{i\sqrt[4]{5}\exp\left(\frac i2\tan^(-1)(2)\right)}{-4i}](https://img.qammunity.org/2023/formulas/mathematics/college/cdja7ytremsds2ka6fowy9neoziz52mo02.png)
![\mathrm{Res}(f(z),z=-1+2i)=\frac{i\sqrt[4]{5}\exp\left(-\frac i2\tan^(-1)(2)\right)}{4i}](https://img.qammunity.org/2023/formulas/mathematics/college/jcdss7n6r29265qmjrkg6sdzwkwi69l3v9.png)
Their sum is
![\displaystyle\sum_(\rm poles)\mathrm{Res}\,f(z)=-\frac{\sqrt[4]{5}}2\sin\left(\frac12\tan^(-1)(2)\right)=-\frac{\sqrt[4]{5}}2\sqrt{(5-\sqrt5)/(10)}=-\frac i2√(\frac1\phi)](https://img.qammunity.org/2023/formulas/mathematics/college/3b197kid7h5ag0qoo8endqv75z0b6leqx3.png)
where ɸ = (√5 + 1)/2 is the golden ratio, and so the overall integral is
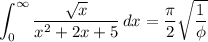
Lastly, recall
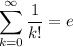
Then our expression reduces to
