Given:
Two chords intersect each other inside the circle.
To find:
The value of x.
Solution:
According to intersecting chords theorem, if two chords intersect each other inside the circle, then the product of two segments of one chord is equal to the product of two segments of second chord.
In the given circle,
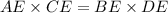
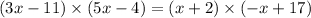
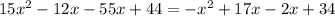
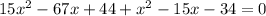
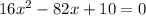
Divide both sides by 2.
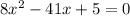
Splitting the middle term, we get

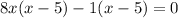
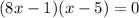
Using zero product property, we get
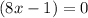 or
or
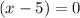
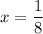 or
or

For
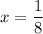 , the side AE is negative. So,
, the side AE is negative. So,
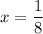 is not possible.
is not possible.
Therefore, the required solution is
 .
.