Question

A trained stunt diver is diving off a platform that is 15 m high into a pool of water that is 45 cm deep. The height, h, in meters, of the stunt diver above the water, is modeled by h=-4.9t^2+12t+5, where t is the time in seconds after starting the dive.

a) How long is the stunt diver above 15 m?

b) How long is the stunt diver in the air?

Answer 1

a) 0 seconds.

b) The stunt diver is in the air for 2.81 seconds.

Explanation:

Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

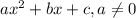This polynomial has roots
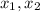`x_(1), x_(2)` such that
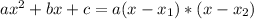`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\Delta))/(2*a)`

`x_(2) = (-b - √(\Delta))/(2*a)`

`\Delta = b^(2) - 4ac`

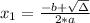
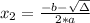
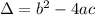
Height of the diver after t seconds:

`h(t) = -4.9t^2 + 12t + 5`

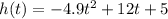
a) How long is the stunt diver above 15 m?

Quadratic equation with
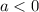`a < 0`, so the parabola is concave down, and it will be above 15m between the two roots that we found for
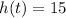`h(t) = 15`. So

`h(t) = -4.9t^2 + 12t + 5`

`15 = -4.9t^2 + 12t + 5`

`-4.9t^2 + 12t - 10 = 0`

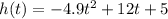
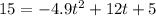
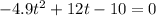
Quadratic equation with
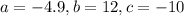`a = -4.9, b = 12, c = -10`. Then

`\Delta = 12^(2) - 4(-4.9)(-10) = -52`

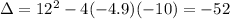
Negative
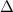`\Delta`, which means that the stunt diver is never above 15m, so 0 seconds.

b) How long is the stunt diver in the air?

We have to find how long it takes for the diver to hit the ground, that is, t for which
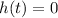`h(t) = 0`. So

`h(t) = -4.9t^2 + 12t + 5`

`0 = -4.9t^2 + 12t + 5`

`-4.9t^2 + 12t + 5 = 0`

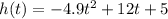
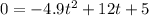
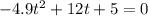
Quadratic equation with
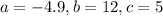`a = -4.9, b = 12, c = 5`. Then

`\Delta = 12^(2) - 4(-4.9)(5) = 242`

`x_(1) = (-12 + √(242))/(2*(-4.9)) = -0.36`

`x_(2) = (-12 - √(242))/(2*(4.9)) = 2.81`

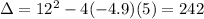
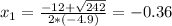
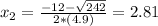
Time is a positive measure, so we take 2.81.

The stunt diver is in the air for 2.81 seconds.