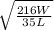Answer:
D =
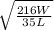
Explanation:
From the given question, the expression showing the relationship among the weight, length and diameter of the metal bar is;
W
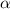 L
L
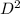
W = kL
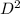
where k is the constant of proportionality.
When W = 140, D = 4 and L = 54, then;
140 = k(54)
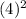
= 864k
k =
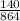
=
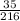
k =
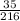
⇒ W =
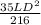
So that;
35L
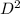 = 216W
= 216W
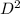 =
=
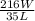
D =