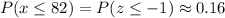Answer: C) 0.16
======================================================
Step-by-step explanation:
Convert the x = 82 to a corresponding z score.
z = (x-mu)/sigma
z = (82 - 89)/7
z = -7/7
z = -1
Using the empirical rule (see chart below), roughly 68% of the distribution is within 1 standard deviation of the mean.
This leaves 1 - 0.68 = 0.32 = 32% of the distribution in both tails, and (32%)/2 = 16% of the area is in one tail, which converts to 0.16
About 16% of the normally distributed population is below z = -1.
So we can say