Answer:
(4,0)
Explanation:
Line segment EG is partitioned by point F in the ratio 1:3.
This means that:
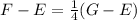
We use this equation to find both the x-coordinate and the y-coordinate of point G.
x-coordinate:
x-coordinate of E: 0
x-coordinate of F: 1
x-coordinate of G: x
Then
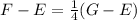
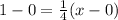
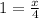
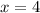
y-coordinate:
y-coordinate of E: 4
y-coordinate of F: 3
y-coordinate of G: y
Then
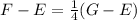
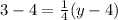
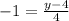
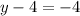
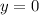
What are the coordinates of point G?
x = 4, y = 0, so (4,0).