Answer:
(a) There is a significant relationship between y and
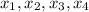
(b)

(c)
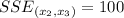
(d)
 and
and
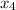 are significant
are significant
Explanation:
Given
 --- estimated regression equation
--- estimated regression equation

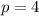 --- independent variables i.e. x1 to x4
--- independent variables i.e. x1 to x4

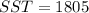
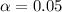
Solving (a): Test of significance
We have:
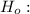 There is no significant relationship between y and
There is no significant relationship between y and
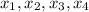
 There is a significant relationship between y and
There is a significant relationship between y and
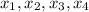
First, we calculate the t-score using:
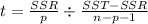
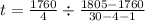
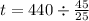
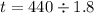
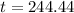
Next, we calculate the p value from the t score
Where:
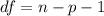
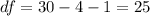
The p value when
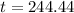 and
and
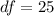 is:
is:
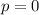
So:
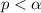 i.e.
i.e.
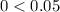
Solving (b):
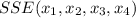
To calculate SSE, we use:
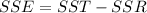
Given that:
 -----------
-----------
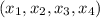
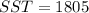
So:
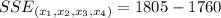

Solving (c):
To calculate SSE, we use:
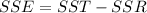
Given that:
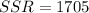 -----------
-----------
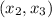
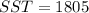
So:
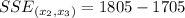
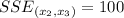
Solving (d): F test of significance
The null and alternate hypothesis are:
We have:
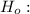
 and
and
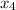 are not significant
are not significant

 and
and
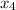 are significant
are significant
For this model:
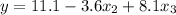
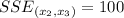
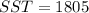
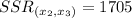

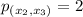
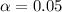
Calculate the t-score
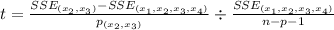

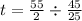
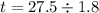
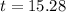
Next, we calculate the p value from the t score
Where:
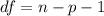
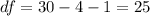
The p value when
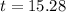 and
and
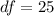 is:
is:
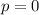
So:
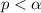 i.e.
i.e.
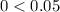
Hence, we reject the null hypothesis