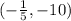Answer:
Explanation:
If the function is
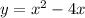 , then its derivative is
, then its derivative is
y' = 2x - 4. This is equal to 0 where
2x - 4 = 0 and
2x = 4 so
x = 2. When x = 2 in the original equation:
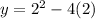 so
so
y = -4. So the coordinate is (2, -4). On to the next one:
If the function is
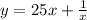 then its derivative is
then its derivative is
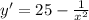 . This is equal to 0 where
. This is equal to 0 where
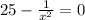 and
and
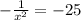 or, in simpler terms:
or, in simpler terms:
 so
so
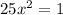 and
and
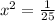 so
so
x = ±
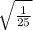 so
so
x =
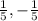 . When you plug those into the original equation, you get the coordinates
. When you plug those into the original equation, you get the coordinates
 and
and