Question

Nina and Jo both ran an 8 km race. Nina took 55 minutes to run the whole race. Jo started the race 3 minutes later than Nina but caught up when they had both travelled 6 km. If Nina and Jo both ran at constant speeds, what is Jo's speed to 2 dp?

Answer 1

Explanation:

First we figure out how fast Nina can run. If Nina can run 8 km in 55 minutes, then her rate is

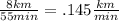`(8km)/(55min)=.145(km)/(min)` and we can use that in a d = rt table:

d = r * t

Nina .145

Jo

Now we can fill in the distance which is 6 for both, since that is the distance where they met:

d = r * t

Nina 6 = .145

Jo 6 =

Now we go to the info given about the time. If Jo started the race 3 minutes after Nina, that means that Nina is running 3 minutes longer than Jo. Filling in the time info:

d = r * t

Nina 6 = .145 * t + 3

Jo 6 = r * t

As you can see, right now we have 2 unknowns in Jo's row. But we don't have to! We will go to Nina's row where the only unknown is time and solve for t. If d = rt, then

6 = .145(t + 3) and

6 = .145t + .435 and

5.55 = .145t so

t = 38.379 minutes. This means that Jo was running 38.379 minutes when she caught up to Nina (it took Nina 3 minutes longer than that to go 6 km since she was already running for 3 minutes when Jo started the race). If Jo's time is 38.379, we can use that in her row for t and solve for r. If d = rt, then

6 = r(38.379) and

r = .16 km/min

Let's check it without the rounding (rounding takes away from the accuracy). If 6 = .145(t + 3) and Nina's rate not rounded is .145454545 and t = 38.37931034, then, rewriting without rounding:

6 should equal .145454545( 38.37931034 + 3)

6 ?=? .145454545(41.37931034)

6 ?=? 6.0 so

Jo's rate is .16 km/min rounded