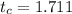Question

Customers at Costco spend an average of $130 per trip (The Wall Street Journal, October 6, 2010). One of Costco's rivals would like to determine whether its customers spend more per trip. A survey of the receipts of 25 customers found that the sample mean was $135.25. Assume that the population standard deviation is $10.50 and that spending follows a normal distribution.A. Specify the appropriate null and alternative hypotheses to test whether average spending at the rival's store is more than $130.B. Calculate the value of the test statistic.C. Calculate the p-value. D. Calculate the critical value

Answer 1

A. The null hypothesis is
`H_0: \mu = 130`.

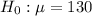The alternative hypothesis is
`H_a: \mu > 130`

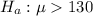
B. The value of the test statistic is
`t = 1`

C. The p-value is of 0.1636.

D. The critical value is
`t_c = 1.711`

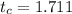
Explanation:

Question a:

Customers at Costco spend an average of $130 per trip (The Wall Street Journal, October 6, 2010). One of Costco's rivals would like to determine whether its customers spend more per trip.

At the null hypothesis, we test if the mean is the same as Costco's, that is:

`H_0: \mu = 130`

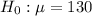
At the alternative hypothesis, we test if the mean is more than 130, that is:

`H_a: \mu > 130`

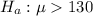
B. Calculate the value of the test statistic.

The test statistic is:

We have the standard deviation for the sample, so the t-distribution is used to solve this question.

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.

130 is tested at the null hypothesis:

This means that
`\mu = 130`

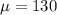
A survey of the receipts of 25 customers found that the sample mean was $135.25. Assume that the population standard deviation is $10.50 and that spending follows a normal distribution.

This means that
`n = 25, X = 135.25, s = 10.50`

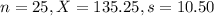
Then

`t = (X - \mu)/((s)/(√(n)))`

`t = (135.25 - 130)/((10.50)/(√(25)))`

`t = 1`

The value of the test statistic is
`t = 1`

C. Calculate the p-value.

Test if the mean is more than a value, so a right-tailed test.

Sample of 25, so 25 - 1 = 24 degrees of freedom.

Test statistic of t = 1.

Using a t-distribution calculator, the p-value is of 0.1636.

D. Calculate the critical value

24 df, using the standard 0.05 significance level.

Using a critical value calculator, the critical value is
`t_c = 1.711`