Answer:
Step-by-step explanation:
From the information given:
The instantaneous expression of the electric field in the wave is:
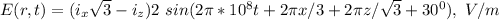
To determine the unit vector in line with the wave electric field, we take the first term in E(r,t) for
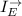 as:
as:
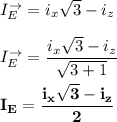
The amplitude is denoted by the numerical value after the first term, which is:
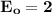
The wavelength can be determined by using the expression:
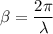
from the given instantaneous expression:
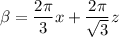
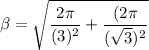
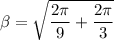
Factorizing 2π
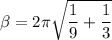
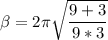
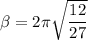
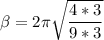
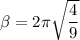
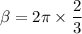
recall from the expression using in calculating wavelength:
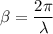
∴
equating both together, we have:
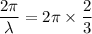
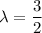
λ = 1.5 m
In line with the wave direction; unit vector
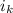 can be computed as follows:
can be computed as follows:
![i_k = - [ \beta_1x +\beta_2z]/\beta](https://img.qammunity.org/2022/formulas/engineering/college/pw8epaguw2eqaoc9iebp8b1l0l5xc62f6o.png)
where;
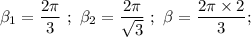
∴
![i_k = - \Big[(2 \pi)/(3)x + (2 \pi)/(√(3)) z\Big]* (1)/((2 \pi *2)/(3))](https://img.qammunity.org/2022/formulas/engineering/college/8cvtsrd8fr6f6tbzfm3e44d01q3xmy3zyr.png)
![i_k = - \Big[(x)/(2) + \sqrt\frac{{3}}{4}} z\Big]](https://img.qammunity.org/2022/formulas/engineering/college/yfiu998xay96sirmo4hbnuja3eks39q0nj.png)
![i_k = - \Big[(1)/(2)x + \sqrt{(3)/(4) }z\Big]](https://img.qammunity.org/2022/formulas/engineering/college/p80ohliv3kbvs2fkgiffo62b8jgk1dcrij.png)
![\mathbf{i_k = - \Big[0.5x +0.86 z\Big]}](https://img.qammunity.org/2022/formulas/engineering/college/ri33c9r1id1v97lqyi5wt8vcgnw54mesee.png)