Question

Lieutenant Commander Data is planning to make his monthly (every 30 days) trek to Gamma Hydra City to pick up a supply of isolinear chips. The trip will take Data about three days. Before he leaves, he calls in the order to the GHC Supply Store. He uses chips at an average rate of seven per day (seven days per week) with a standard deviation of demand of two per day. He needs a 98 percent service probability.

Required:
If he currently has 35 chips in inventory, how many should he order? What is the most he will ever have to order?

Answer 1

219.57 units

Step-by-step explanation:

Given :

Daily demand, d = 7 per day

Standard deviation, = 2 per day

Service probability = 98%

Total number of days per week = 7

Lead time , L = 3 days

On hand inventory, I = 35

Now calculating the optimal order quantity by using the given formula,

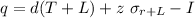`$q=d(T+L)+ z \ \sigma_(r+L)-I$` .............(i)

First, we will find out the value of
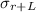`$\sigma_(r+L)$` and z.

Therefore,

`$\sigma_(r+L)=√((30+3)(2)^2)$`

`$=√(132)$`

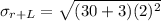
= 11.48

Now the value of z can be found out from the z-table,

Z value for 98% service level = 2.054

Now putting the value of
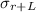`$\sigma_(r+L)$` and z in equation (i), we get,

`$q=d(T+L)+ z \ \sigma_(r+L)-I$`

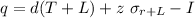
= (7)(30+3)+(2.054)(11.48) - 35

= 231 + 23.57 - 35

= 219.57 units

So the optimal number of the units required to be order = 219.57 units