Question

1. A researcher would like to compare the effectiveness of video versus reading for communicating information to adolescents. A sample of n1= 10 adolescents is given a pamphlet explaining nuclear energy and told that they will be tested on the information. A separate sample of n2= 10 adolescents is shown a video that contains the same information presented in a fast-paced visual form and told that they will be tested. One week later all 20 subjects are given a test on nuclear energy. The average score for the pamphlet group was 1= 51 with s12= 16. The video group averaged 2= 46 with s22= 20. Conduct a t-Test (two-tail, α = .05) for two Independent groups to see if there is a significant difference between the two groups (follow the Handout).

Answer 1

There is significant statistical evidence to suggest there is a difference between the groups

Explanation:

The number of adolescents in the sample that were given a pamphlet, n₁ = 10

The average score of those given a pamphlet,
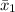`\bar x_1` = 51

s₁² = 16

The number of adolescents in the sample that were given a video, n₂ = 10

The average score of those given a video,
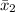`\bar x_2` = 46

s₂² = 20

The alpha level of the test, α = 0.05

H₀ = No difference

Hₐ = Difference between the groups

The test statistic for the difference in mean is given as follows;

`t=\frac{(\bar{x}_1-\bar{x}_(2))}{\sqrt{(s_(p)^(2) )/(n_(1))+(s _(p)^(2))/(n_(2))}}`

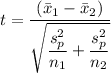
Plugging in the values, gives;

`t=\frac{(46-55)}{\sqrt{(18 )/(10)+(18)/(10)}} \approx -4.73`

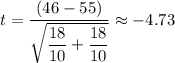
The degrees of freedom, n₁ + n₂ - 2 = 20 - 2 = 18

The critical-t = 2.101

Therefore

Given that the test statistic is larger than than the critical-t, we reject the null hypothesis that there is no difference