Answer:
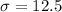 ---- sample standard deviation
---- sample standard deviation
 ---- sample variance
---- sample variance
Explanation:
Solving (a): The sample variance
First, we calculate the midpoint of each class (this is the average of the limits)
So, we have:
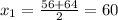
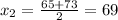
And so on
So, the table becomes:

Calculate the mean
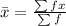

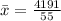
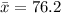
The variance is:
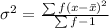
So, we have:
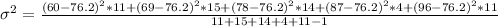
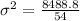

The sample standard deviation is:
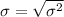
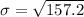
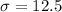
Solving (b): The sample variance
In (a), we calculate the sample variance to be:
