Answer:
∠B = 74°
a ≈ 14.5 inches
c ≈ 11.4 inches
Explanation:
The given parameters of triangle ΔABC are;
∠A = 62.2°, ∠C = 43.8° and side
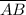 = b = 15.8 in
= b = 15.8 in
By sine rule, we have;
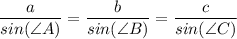

By angle sum property, we have;
∠B = 180° - (∠A + ∠C)
∴ ∠B = 180° - (62.2° + 43.8°) = 74°
∠B = 74°
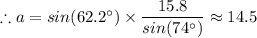
a ≈ 14.5 in.
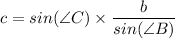

c ≈ 11.4 in.