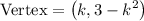Question

If k is a non-zero constant, determine the vertex of the function y = x2 - 2kx + 3 in terms of k.

Answer 1

Set y = 0, evaluate the quadratic at h=−b2a and solve for k.

k=9 I think..... I'm not completely sure but I think that's how it is

Answer 2

`\displaystyle \text{Vertex} = \left(k, 3-k^2\right)`

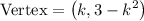
Explanation:

We are given the quadratic equation:

`y=x^2-2kx+3`

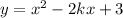
Where k is a non-zero constant.

And we want to determine the vertex of the parabola in terms of k.

The vertex of a parabola is given by the formulas:

`\displaystyle \text{Vertex}=\left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

In this case, a = 1, b = -2k, and c = 3.

Find the x-coorinate of the vertex:

`\displaystyle x=-((-2k))/(2(1))=(2k)/(2)=k`

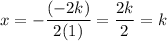
To find the y-coordinate, we substitute the value we acquired back into the equation. So:

`\displaystyle \begin{aligned} y(k)&=(k)^2-2k(k)+3\\&=k^2-2k^2+3\\&=3-k^2\end{aligned}`

Therefore, our vertex in terms of k is:

`\displaystyle \text{Vertex} = \left(k,3-k^2\right)`