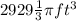Answer:
The volume of this sphere is equal to
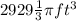
Explanation:
In order to solve this question, we need to know the formula for the volume of a sphere which is...
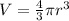 ("V" is the volume of the sphere, and "r" is the radius of the sphere)
("V" is the volume of the sphere, and "r" is the radius of the sphere)
Now we have to substitute the values that we already know into the formula, and we will get that...

Therefore, the volume of this sphere is equal to