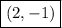Answer:
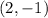
Explanation:
Given the system of equations:
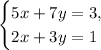
Multiply the first equation by -2 and the second equation by 5, then add both equations to solve for
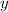 :
:
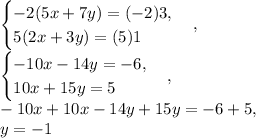
Substitute
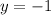 into any equation to solve for
into any equation to solve for
 :
:
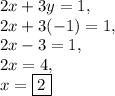
Therefore, the solution to this system of equations is