Question

Point A has coordinates (-24, -54)

Point B has coordinates (40, -46)
Find the equation of the perpendicular bisector of line AB.
ANSWER ASAP

Answer 1

`y=-8x+14`

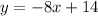
Explanation:

Hi there!

What we need to know:

• A perpendicular bisector of a line segment is 1) perpendicular to the line segment and 2) passes through the midpoint of the line segment
• Perpendicular lines always have slopes that are negative reciprocals (ex. -2 and 1/2)
• Linear equations are typically organized in slope-intercept form:
  `y=mx+b` where m is the slope and b is the y-intercept (the value of when x is 0)

1) Determine the midpoint of the line segment

Midpoint:
`((x_1+x_2)/(2) ,(y_1+y_2)/(2) )` where the coordinates of the endpoints are
`(x_1,y_1)` and
`(x_2,y_2)`

Plug in the endpoints (-24, -54) and (40, -46)

`((-24+40)/(2) ,(-54+(-46))/(2) )\\((-24+40)/(2) ,(-54-46)/(2) )\\((16)/(2) ,(-100)/(2) )\\(8 ,-50)`

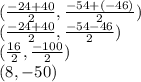
Therefore, the midpoint of line AB is (8,-50).

2) Determine the slope of the line segment

This will help us find the equation of the perpendicular bisector.

slope =
`(y_2-y_1)/(x_2-x_1)` where two given points are
`(x_1,y_1)` and
`(x_2,y_2)`

Plug in the endpoints (-24, -54) and (40, -46)

`= (-46-(-54))/(40-(-24))\\= (-46+54)/(40+24)\\= (8)/(64)\\= (1)/(8)`

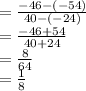
Therefore, the slope of line AB is
`(1)/(8)`.

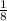3) Determine the slope of the perpendicular bisector

Because perpendicular lines always have slopes that are negative reciprocals, the slope of the perpendicular bisector is -8 (the negative reciprocal of 1/8). Plug this slope into
`y=mx+b`:

`y=-8x+b`

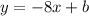
4) Determine the y-intercept (b) of the perpendicular bisector

`y=-8x+b`

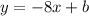
Recall that we found the midpoint of line AB, (8,-50). The perpendicular bisector passes through this point. Plug (8,-50) into
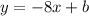`y=-8x+b` and solve for b:

`-50=-8(8)+b\\-50=-64+b`

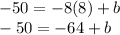
Add 64 to both sides to isolate b

`-50+64=-64+b+64\\14=b`

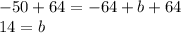
Therefore, the y-intercept of the line is 14. Plug this back into
`y=-8x+b`:

`y=-8x+14`

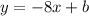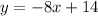
I hope this helps!