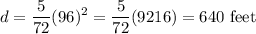Answer:
640 feet.
Explanation:
Let d represent the distance required to stop and let s represent the speed of the car.
The distance required to stop varies directly as the square of its speed. In other words:
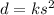
Where k is the constant of variation.
250 feet are required to stop a car traveling 60 miles per hour. Substitute:
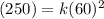
Simplify and solve for k:
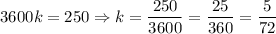
So, our equation is:
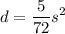
Then the distance required to stop a car traveling 96 miles per hour will be: