Answer:
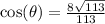
=================================================
Work Shown:
x^2+y^2 = r^2
(8)^2+(-7)^2 = r^2
113 = r^2
r = sqrt(113)
The distance from (0,0) to (8,-7) is exactly sqrt(113) units.
This is the exact length of the hypotenuse of the right triangle.
Next, we do the following steps:
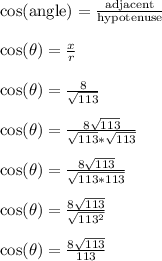
Side note: cosine is positive in quadrant Q4.