Question

The height of a triangle is 4 feet more than 3 times the base. If the area is 112 ft find the base and height of the triangle

Answer 1

`base = 8 ft\\height =28 ft\\`

Explanation:

let base be x ft. then the height is 3x+4

`Area=(1)/(2) * x * (3x+4)=112\\3x^(2) +4x=224\\3x^(2) +4x-224=0\\x=8, x=-9.33 (no sol. as length can not be negative)\\ x=8\\base = 8 ft\\height =3(8)+4=28 ft\\`

Answer 2

base = 8 , height = 28

Explanation:

Let base be = b

Given:

height is 3times base = 3b

Also 4 feet more than 3 times base = 3b + 4

Area = 112 square feet

`area = (1)/(2) * base * height\\\\112 = (1)/(2) * b * (3b+ 4)\\\\224 = b(3b+4)\\\\224 = 3b^2 + 4b\\\\3b^2 + 4b - 224 = 0\\\\`

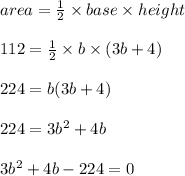
The quadratic equation with a = 3 , x = 4 , c = -224

Therefore ,

`b = (-x \pm √(x^2 - 4ac))/(2a)\\\\`

`b= (-4 \pm √(4^2 - (4 * 3 \imes -224)))/(2 * 3)\\\\b= (-4 \pm √(16 + 2688))/(6)\\\\b= (-4 \pm √(2704))/(6)\\\\b= (-4 \pm52 )/(6)\\\\b = (-4 + 52)/(6) , \ b = (-4 -52)/(6)\\\\b = (48)/(6) , \ b = -(56)/(6)`

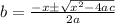
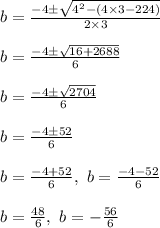
Since base can't be negative base = 8 ft

Therefore , height = 3b + 4 = 3(8) + 4 = 24 + 4 = 28