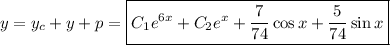Start with the underlying homogeneous equation:
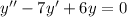
which has characteristic equation
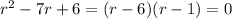
with roots at r = 6 and r = 1. So the characteristic solution is

Now for the particular solution, we can use the method of undetermined coefficients, with the following ansatz (the "guess" solution) and its derivatives,
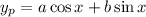
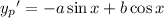
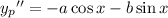
Substituting these into the original equation gives
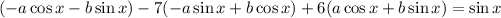
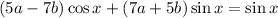

So the particular solution is
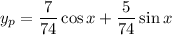
and hence the general solution is