Answer:
Limit=0
Converges
Absolutely converges
Explanation:
If

then
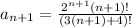 .
.
Let's rewrite
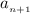 a little.
a little.
I'm going to hone in on (3(n+1)+4)! for a bit.
Distribute: (3n+3+4)!
Combine like terms (3n+7)!
I know when I have to find the limit of that ratio I'm going to have to rewrite this a little more so I'm going to do that here. Notice the factor (3n+4)! in
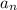 . Some of the factors of this factor will cancel with some if the factors of (3n+7)!
. Some of the factors of this factor will cancel with some if the factors of (3n+7)!
(3n+7)! can be rewritten as (3n+7)×(3n+6)×(3n+5)×(3n+4)!
Let's go ahead and put our ratio together.
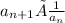
The second factor in this just means reciprocal of
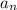 .
.
Insert substitutions:
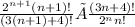
Use the rewrite for (3(n+1)+4)!:
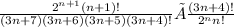
Let's go ahead and cancel the (3n+4)!:
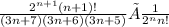
Use 2^(n+1)=2^n × 2 with goal to cancel the 2^n factor on top and bottom:
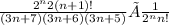
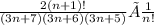
Use (n+1)!=(n+1)×n! with goal to cancel the n! factor on top and bottom:

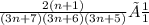
Now since n approaches infinity and the degree of top=1 and the degree of bottom is 3 and 1<3, the limit approaches 0.
This means it absolutely converges and therefore converges.